Bloom Filter

19 Mar 2017

Introduction

The world is full of interesting data structures. Today I want to cover the Bloom Filter, which is actually quite simple but it took me a bit to get the idea.
Basically, is a probabilistic data structure that using a significant small amount of space let us know if an element is in a set. Well not exactly that. It can tell us two things:

• The element may be in the set.
• The element is definitely not in the set.

And that’s all it can do well.

Uhm, definitely it looks curious. “May be in the set?” Usually we work with data structures that tell us things for sure. But that is the cost of using much less space. Let’s have a look.

Structure

We are going to start with a hash table. I suppose that you know how a hash table works. This hash table has N buckets. And each bucket consists of a 1-bit boolean (actually this is a Bit Vector). So the size of the table is N/8 bytes.
Very fast hash functions are important to ensure a fast Bloom Filter. We are going to use more than one hash function to ensure that we reduce false positives. For example the functions SipHash and Fnv look interesting.

Essentially we are going to apply the hash functions to the element that we are inserting. Each function will return an index in the table. And all we have to do is to mark as true that bit of the table if is not true yet.

The process is pretty much the same to ask for an element. We apply the hash functions and we obtain the index. If any of the bits is false, it is definitely not in the set. And if all the bits are true, it might be. Why? That’s because those bits could have been marked by the insertion of that element or by another element which has produced a similar hash code. So we are not sure. The more collisions we have the more likely we obtain false positives.

Example

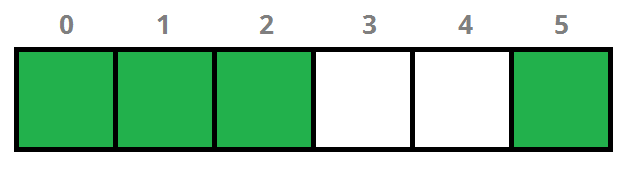
Let’s look at this example. We have a Bloom Filter of N=6 and two hash functions (h1 and h2), where we’ve inserted a few words and these are the hash that they have produced:

	"ever"	"rain"	"have"
h1	2	5	1
h2	0	2	5

Our Bloom Filter looks like this:
Now, if we ask for the element “seen”:
h1("seen") = 3, h2("seen") = 0
We can see that one of those bits is set to false, so “seen” is not in the set. However, if we ask for the element “you”:
h1("you") = 0, h2("you") = 5
We can see the that both bits are marked as true. So “you” can be in the set. Although obviously we know that it is not in the set.

False Positives

Ok, but now we want to know how we can choose the size of our Bloom Filter so that we can obtain a reasonable false positives rate. Actually the chance of a false positive is approximately:

$$(1-e^{-kn/m})^k$$

Where n is the amount of elements in the set, m the number of buckets and k the number of hash functions used. You must choose the parameters according to your needs.

Implementation

I’ve developed a simple implementation in C++ to play with it.
Implementation in C++