Fylux Things

Finding Holes Fast

07 Apr 2017

Introduction

Suppose a directed graph. We will define “hole” as a node that doesn’t point at any node and it’s pointed by every node of the graph (except itself).

The task is to find all the holes in a graph, given a common adjacency matrix or adjacency list. A common one. No data structure changes are allowed. And we want to find it in linear time, . Ambitious, isn’t it?

By the way, maybe you prefer to think about how to solve it before seeing the solution. It’s neither trivial nor impossible.


Simplifying

First of all, we should analyze the problem, so maybe we can make it simpler. We are searching holes, but, how many holes can exist in a graph? Actually, only one. Why?

Remember the definition of hole. It’s pointed by every node and it doesn’t point at any node. Suppose we had two holes, A and B. Because they are holes, they must be pointed by all the nodes. Which means that A must be pointed by B and vice versa. But if it they point at each other they are pointing to a node, so they can’t be holes.

First lemma: A graph has one or none holes.


Common idea

I guess that everybody would start taking a look at the graph to see how a graph with a hole looks like. Me too.

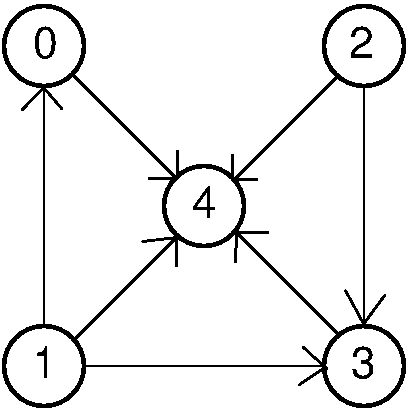
I’m going to consider the two data structures, a list and a matrix. First we should analyze how each of these structures looks when the node n is a hole.

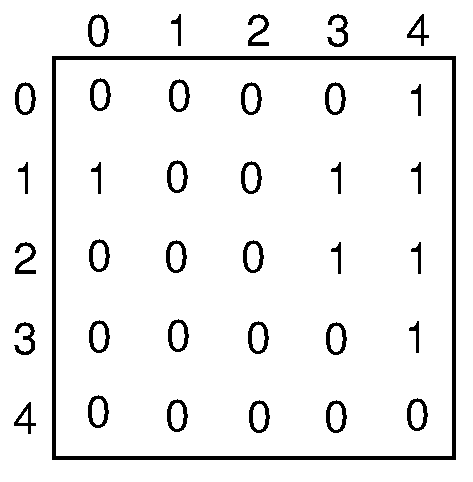
  • Matrix: The nth row is full of zeros and the nth column full of ones, except [n][n]

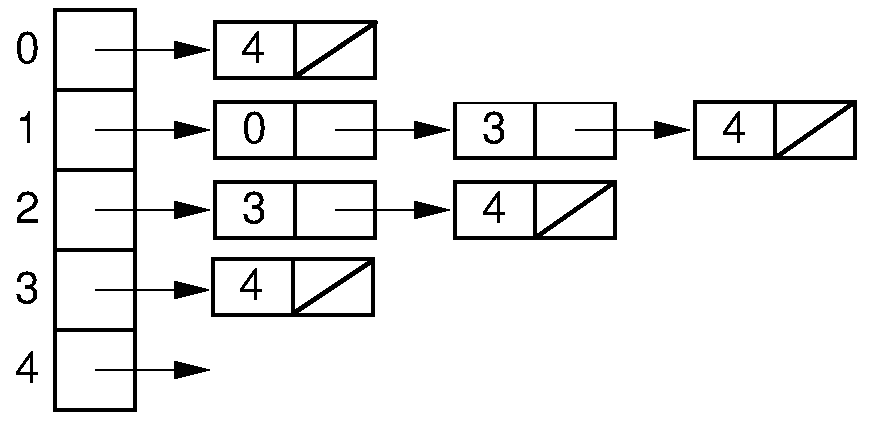
  • List: The nth list has no elements and every other list has the element n. I consider the operation to obtain how many elements are in a list.

Matrix

So the first idea is to search for a row full of zeros in the matrix and then check if its column is full of ones. Unfortunately, we can notice easily that this search has .

List

Pretty much the same with lists. First we look for a list n without elements and then we look for that n in each other list. We know that if there is more than one list without elements, there cannot be a hole. But if there is a hole the algorithm has , which is the cost of looking for n in all the lists.


Think Different

Let’s think in a different way. Forget about how holes look in the structures and think about the relationship between nodes. We know the definition of hole. So given two nodes of the graph and their corresponding edge, can we know if any of them is a hole? The answer is yes.

There are 3 possible scenarios:

  • Node x points at Node y -> Node y may be a hole
  • Node x points at Node y and vice versa -> None of them is a hole
  • There is no edge -> None of them is a hole.

Therefore, an interesting approach is to compare nodes in pairs and discard nodes. Finally, you will have no candidates or only one candidate. Then you just have to check if that last candidate is a hole taking a look at its row and column.


Example

Let’s try this idea with our example graph and an adjacency matrix.

  • Take node 0 and node 1.
  • Node 1 points at node 0, so 0 may be a hole.
  • Take node 0 and node 2.
  • There is no edge, so none of them is a hole.
  • Take node 3 and 4.
  • Node 3 points at node 4, so 4 may be a hole.

Finally we see that our last candidate is node 4, and if we check its row and column we can confirm that it is a hole.

Implementation

I’ve developed an implementation of this algorithm to show how our reasoning works:

Implementation in C++
Implementation in Python

Related Posts