List vs Vector: A Performance Comparison

29 Jun 2017

Introduction

I would dare to say that linked lists and vectors are the most widely used data structures. Supposedly, we all know which one is better of each task so we can choose wisely. However, the reasoning for choosing a data structure is mostly based in the famous Big-O notation. Unfortunately, this notation doesn’t consider the details of computers so it could lead us astray.

In this article, I am going to compare the performance of linked lists against vectors when we want to store elements in order of insertion (push_back). This is one of the few cases where I consider linked lists to be a good choice. I won’t cover random insertion and elimination because there is no doubt about the poor performance of vectors in that case.

I can recommend lots of comparisons like this one comparing the performance of different data structures with respect to the number of elements. However, this doesn’t show us the reasons and the results that we are looking for. Instead, I will try to explain the aspects that can affect their performance and how to choose the best option according to these factors, avoiding easy conclusions.

Thinking

Let’s start thinking about which results should be expected.

Algorithmics

If we have a double linked list or a linked list with a pointer to the end of the list, the cost of inserting an element at the end will be constant. There is no doubt about it; this process will be always the same.

Nevertheless, it is quite different in vectors. If we are using arrays, we can’t have many chunks of memory connected by pointers, we can only have a big chunk of contiguous memory. This means that if we want to have the same memory occupied as elements are stored we will have to reallocate all the memory in each insertion. But, reallocating has a linear cost that we cannot tolerate in each insertion. However, this problem is well known and vectors usually reserve more memory than it’s needed to prevent it. The most common strategy once the array is full is to reserve a new array twice the capacity. Obviously, this will affect the memory usage of our program but it’s something that we will discuss later.

Therefore we can suppose that the performance of lists will be better than vectors, because the latter’s worst case requires linear time, although it occurs only when is full; but hey, lists doesn’t have this drawback.

Architecture

As I said before, theory isn’t everything. Modern computers performance depends on many factors. Some of the most important are cache misses and space locality. If you are not familiar with this topic I recommend you to take look at this explanation. But basically, what we are looking for is having as much useful information per memory block as possible. And don’t overlook the word useful.

When we use arrays is well known that all the data is contiguous and therefore no pointers are required. This means that a memory block will be completely filled with the elements of the array.

However, when we use linked lists we need to store pointers next to each element of the list. Therefore, in a block of memory we will find pointers and elements. Unfortunately, these pointers will occupy memory that could be filled by more elements. The effect that it will have on performance will depend on the size of the elements.

In most 64 bits computers, pointers occupy 8 bytes of memory. That is quite a lot. If you are using a double linked list like C++ STL list you will be using 16 bytes for pointers per element. Thus if you store in each node 1 MB you won’t notice the size of pointers and it won’t matter when using a memory block. However, the common case is having small size elements, because when we work with big amounts of data we tend to use pointers. For example when we have a linked list of strings, we don’t store all the chars, just a pointer to the char array.

Furthermore, each insertion in a linked list requires allocating dynamic memory, which is not immediate. Hence linked lists don’t look so nice when working with small elements.

Performance

As we have seen, it’s not clear what results should be expected. The benefits of vectors related with space locality are clear, but we don’t know how the cost of reallocating all the elements will affect when it’s full.

In our first test we will compare the time required to store 1,100,000 8 bytes elements in a list and a vector. This number has been specifically chosen to unsure that we will reallocate the vector almost just after finishing because it’s a bit more than 2²⁰.

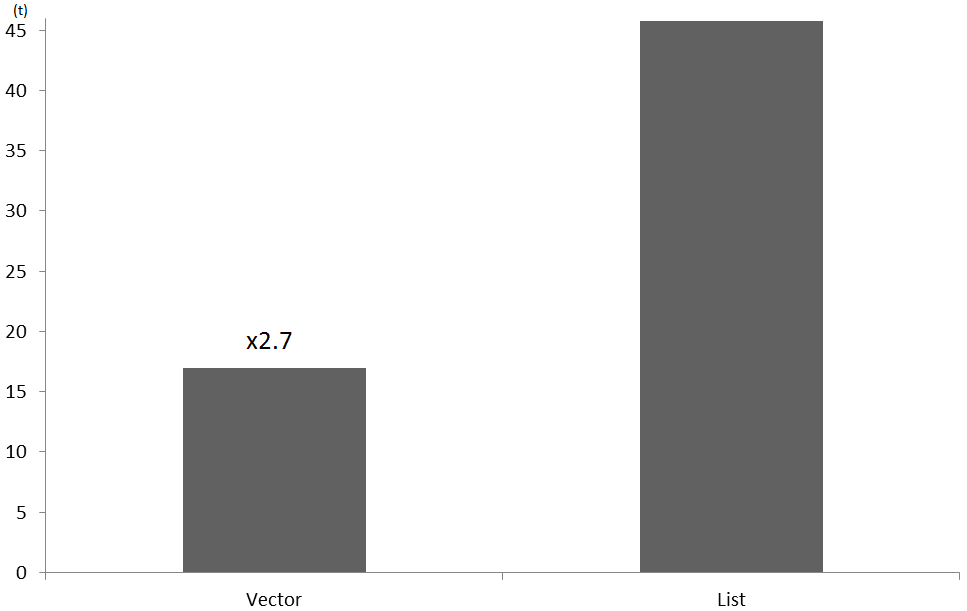
Undoubtedly, the performance of vectors in this case is way better than lists.

Although I could have stopped here, I wanted to see how this evolves when changing the size of the elements stored. (Inserting 100,000 elements)

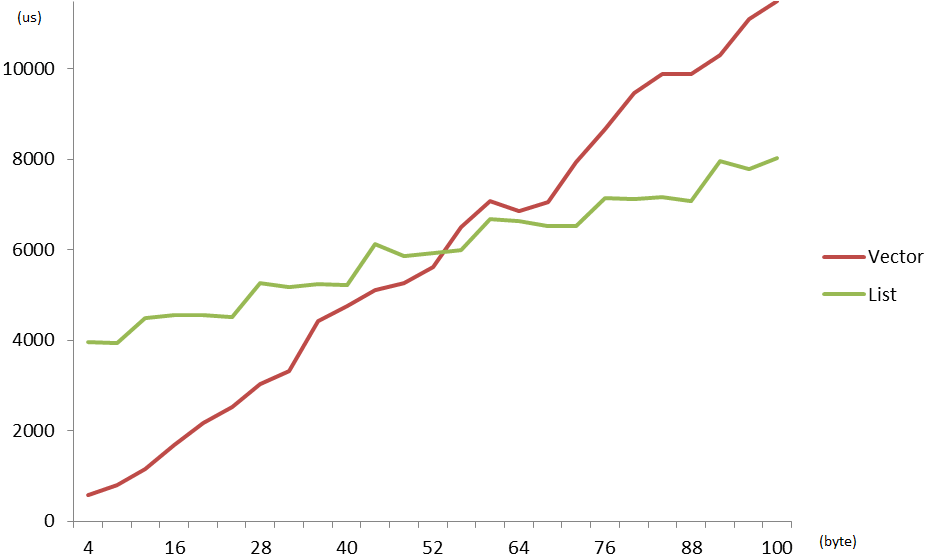
This is such as an interesting graph. It’s telling us which data structure is better depending on the size of the elements. As expected the performance of the vector decreases because of the cost of reallocating so much data, while the performance of the linked list with respect to the vector improves as the elements size increases.

Memory usage

Although I’ve focused on analyzing the performance of these structures, I think that we should also take a look at the memory usage. Unlike speed, memory usage is way more clear how will it behave. Hereinafter we will refer to the number of elements as n and to the size of the element as m.

The size occupied by a double linked list is given by m plus two times the size of the pointer. Because the size of the pointer is expected to be 8 bytes, we can ensure that the memory used per element will be at least 16 bytes.

$$n \cdot (16+m)$$

On the other hand, the memory occupied by a vector depend on how much memory are we reserving. For this analysis, I’m going to consider the most widely used implementation of vector from C++ STL. This one reserves twice the space required to store the elements. Therefore, the memory used by our vector is given by:

$$m \cdot 2^{\lceil{log_2 {n}}\rceil}$$

This means that we will be using between s and 2s bytes to store the elements, being s the exactly amount of data required to store the information.

Furthermore, we can find which structure will be using less memory for a given element size formulating the following inequality:

$$m \cdot 2^{\lceil{log_2 {n}}\rceil} <> n \cdot (16+m)$$

Hence you can easily find which structure will require less memory. I wanted to illustrate this with a graph. We will insert 100,000 elements for different element sizes, to see how memory usage changes.

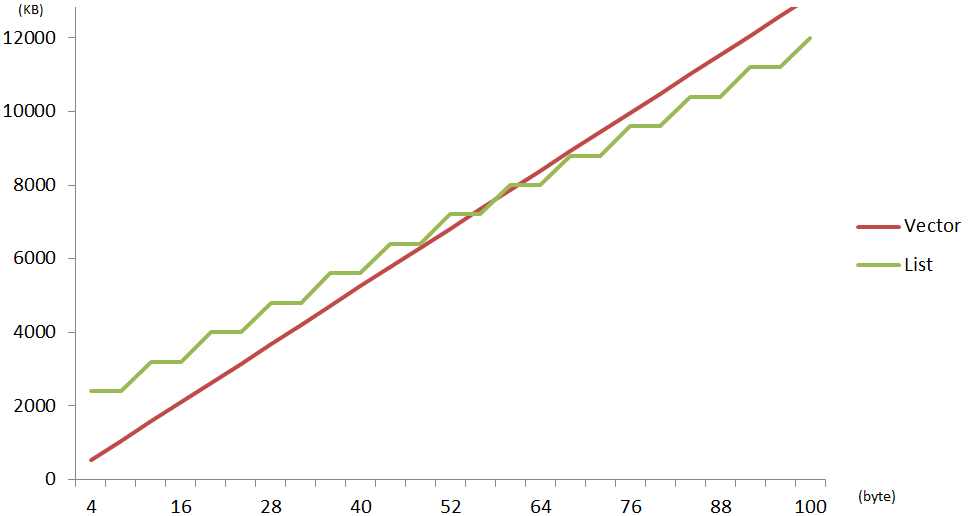
What a nice graph. As you can see there is a point where lists start to use less memory than vectors. Not only that, we can easily notice that the point where one structure overtake the other is almost the same point that we saw in the speed graph. Therefore, if you choose the right structure you will not only obtain the best performance but also the lower memory usage.

Padding

Before concluding, I must say that I’ve been bitting my tongue along the last paragraphs to avoid complicating the explanation.

You have probably notice the curious stepped form of the curve of list memory usage. The truth is that linked lists have one more drawback, which is the padding caused because of memory alignment. I don’t intend to explain this problem, but basically, if you are using 8 byte pointers the memory used per element will be always a multiple of 8 even if it should be lower. Therefore, if we store a single-byte char, instead of needing 17 bytes we will need 24 bytes.

If you want to dig deeper into this topic you can start here.

One last thing

In this article I’ve worked with memory-contiguous linked lists. However, often this won’t be the case. The negative effects of dispersed linked lists will be studied in future articles.

Conclusion

After this analysis I guess that there is no doubt about which data structure is better for this particular case. However, I hope that this analysis is not only useful for choosing between lists and vectors but also for understanding which elements may affect the performance of data structures and how to analyze them for your personal purposes.

Code

The code used and the tests developed in this article can be found here as well as the hardware and software used.